近日，我院微纳电子材料与新型信息器件课题组曾波文博士和华中科技大学胡勇教授团队合作，在关于玻色型BdG系统中非厄米AB笼中简并类型的区分取得进展。研究团队在玻色型BdG系统中构造具有多种简并平坦带(DFBs)的非厄米AB笼，通过传输矩阵阐明简并平坦带的简并类型、最小多项式之间的对应关系，且基于这种对应关系，提出了一种实现高简并平带的方案。相关成果以《Non-Hermitian Aharonov-Bohm cage in bosonic Bogoliubov-de Gennes systems》为题发表于凝聚态物理顶级期刊《Physical Review B》。华中科技大学周琨棱博士为第一作者，我院曾波文博士和华中科技大学胡勇教授为共同通讯作者，长沙理工大学为共同通讯单位。

   

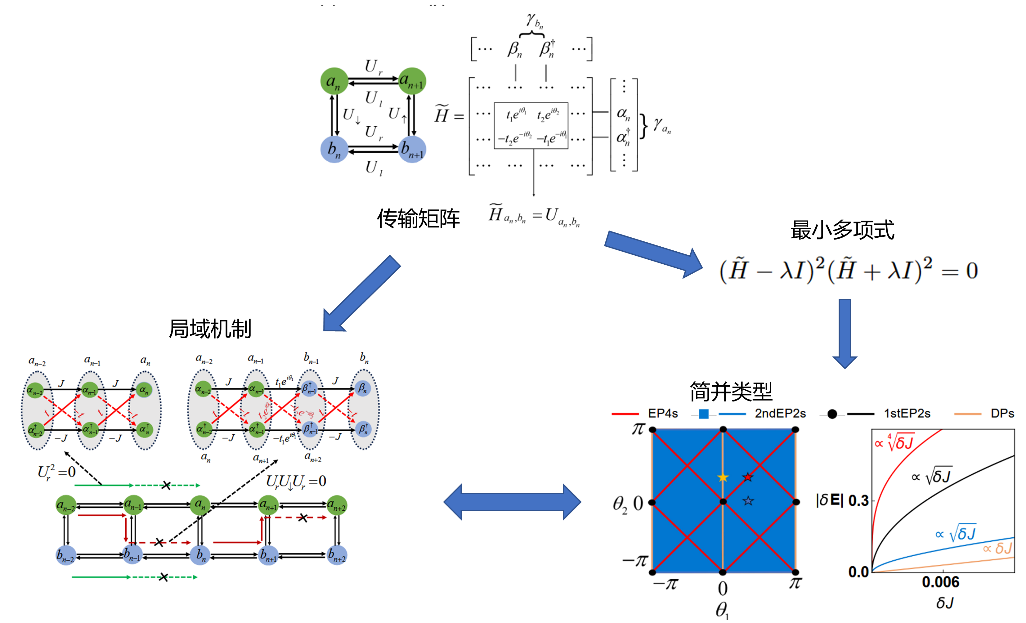
图1. 传输矩阵、局域机制和平带简并类型的对应关系。

非厄米阿哈罗诺夫-玻姆(AB)笼是一种独特的局域化现象，它能束缚所有可能的激发。这种束缚作用导致动量空间中出现完全平坦的能谱，而这类能谱通常伴随多种类型的简并。对简并类型进行分类对于研究非厄米AB笼的动力学性质至关重要，但相关的分类方法及其物理关联仍不明确。在这一基于玻色型BdG系统构建的非厄米AB笼中，通过调控系统参数，我们实现了对平坦带简并类型的灵活操控，其简并类型可从Dirac点(DPs)型调控至高阶奇异点(EPs)型。与传统上通过对外界微扰的响应来区分简并类型的方法不同，本文建立了参数依赖的转移矩阵与最小多项式之间的对应关系，可用于判定简并平坦带的简并类型。

该项工作得到了湖南省自然科学基金和Innovation Program for Quantum Science and Technology项目的支持。

文章链接：https://journals.aps.org/prb/abstract/10.1103/y174-pms8

（ 图文/伍丹 一审/范志强 二审/刘斯 三审/张国强）